
| Scientific journal of the theoretical and applied researches |
Print ISSN 1561-9443 On-line ISSN 1561-9451 |
| Issues list | |||
| Content of 1(11) 1999 | |||
| Mathematics and Computer Science | |||
| Physics | |||
| New Educational Technologies | |||
1(11)
|
|
Print Edition of "The News of Altai State University" © 1996-2010 Altai State University.
All rights reserved. Any of parts of a journal or edition as a whole cannot be reprinted without the written sanction of the authors or publisher. On purchase of a journal to address to ASU publishing house: Altai State University. 656049, 66 Dimitrova street, Barnaul, Russia. Telephone + 7 (3852) 366351. |
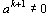 where (k+2) - index of nilpotency of algebra R.
where (k+2) - index of nilpotency of algebra R.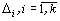 , which constructed from coefficients of the main relations of this algebras:
, which constructed from coefficients of the main relations of this algebras: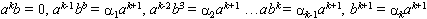 (1)
(1)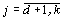 for some d. Then R is a C-algebra if and only if
for some d. Then R is a C-algebra if and only if 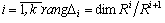 for any
for any 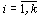 .
.